티스토리 뷰
그리디 문제다.
내가 푼 방법은 테스트케이스 17번 딱 하나가 시간초과로 절대 풀리지 않았다.
그러던 중 질문하기 탭에서 엄청난 풀이를 발견했다. !!!
그래서 그 풀이를 정리해보려고 한다.
문제
https://school.programmers.co.kr/learn/courses/30/lessons/150369
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명
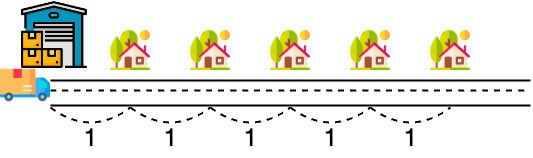
당신은 일렬로 나열된 n개의 집에 택배를 배달하려 합니다. 배달할 물건은 모두 크기가 같은 재활용 택배 상자에 담아 배달하며, 배달을 다니면서 빈 재활용 택배 상자들을 수거하려 합니다.
배달할 택배들은 모두 재활용 택배 상자에 담겨서 물류창고에 보관되어 있고, i번째 집은 물류창고에서 거리 i만큼 떨어져 있습니다. 또한 i번째 집은 j번째 집과 거리 j - i만큼 떨어져 있습니다. (1 ≤ i ≤ j ≤ n)
트럭에는 재활용 택배 상자를 최대 cap개 실을 수 있습니다. 트럭은 배달할 재활용 택배 상자들을 실어 물류창고에서 출발해 각 집에 배달하면서, 빈 재활용 택배 상자들을 수거해 물류창고에 내립니다. 각 집마다 배달할 재활용 택배 상자의 개수와 수거할 빈 재활용 택배 상자의 개수를 알고 있을 때, 트럭 하나로 모든 배달과 수거를 마치고 물류창고까지 돌아올 수 있는 최소 이동 거리를 구하려 합니다. 각 집에 배달 및 수거할 때, 원하는 개수만큼 택배를 배달 및 수거할 수 있습니다.
다음은 cap=4 일 때, 최소 거리로 이동하면서 5개의 집에 배달 및 수거하는 과정을 나타낸 예시입니다.
배달 및 수거할 재활용 택배 상자 개수
집 #1집 #2집 #3집 #4집 #5| 배달 | 1개 | 0개 | 3개 | 1개 | 2개 |
| 수거 | 0개 | 3개 | 0개 | 4개 | 0개 |
배달 및 수거 과정
집 #1집 #2집 #3집 #4집 #5설명| 남은 배달/수거 | 1/0 | 0/3 | 3/0 | 1/4 | 2/0 | 물류창고에서 택배 3개를 트럭에 실어 출발합니다. |
| 남은 배달/수거 | 1/0 | 0/3 | 3/0 | 0/4 | 0/0 | 물류창고에서 5번째 집까지 이동하면서(거리 5) 4번째 집에 택배 1개를 배달하고, 5번째 집에 택배 2개를 배달합니다. |
| 남은 배달/수거 | 1/0 | 0/3 | 3/0 | 0/0 | 0/0 | 5번째 집에서 물류창고까지 이동하면서(거리 5) 4번째 집에서 빈 택배 상자 4개를 수거한 후, 수거한 빈 택배 상자를 물류창고에 내리고 택배 4개를 트럭에 싣습니다. |
| 남은 배달/수거 | 0/0 | 0/3 | 0/0 | 0/0 | 0/0 | 물류창고에서 3번째 집까지 이동하면서(거리 3) 1번째 집에 택배 1개를 배달하고, 3번째 집에 택배 3개를 배달합니다. |
| 남은 배달/수거 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 3번째 집에서 물류창고까지 이동하면서(거리 3) 2번째 집에서 빈 택배 상자 3개를 수거한 후, 수거한 빈 택배 상자를 물류창고에 내립니다. |
16(=5+5+3+3)의 거리를 이동하면서 모든 배달 및 수거를 마쳤습니다. 같은 거리로 모든 배달 및 수거를 마치는 다른 방법이 있지만, 이보다 짧은 거리로 모든 배달 및 수거를 마치는 방법은 없습니다.
트럭에 실을 수 있는 재활용 택배 상자의 최대 개수를 나타내는 정수 cap, 배달할 집의 개수를 나타내는 정수 n, 각 집에 배달할 재활용 택배 상자의 개수를 담은 1차원 정수 배열 deliveries와 각 집에서 수거할 빈 재활용 택배 상자의 개수를 담은 1차원 정수 배열 pickups가 매개변수로 주어집니다. 이때, 트럭 하나로 모든 배달과 수거를 마치고 물류창고까지 돌아올 수 있는 최소 이동 거리를 return 하도록 solution 함수를 완성해 주세요.
제한사항
- 1 ≤ cap ≤ 50
- 1 ≤ n ≤ 100,000
- deliveries의 길이 = pickups의 길이 = n
- deliveries[i]는 i+1번째 집에 배달할 재활용 택배 상자의 개수를 나타냅니다.
- pickups[i]는 i+1번째 집에서 수거할 빈 재활용 택배 상자의 개수를 나타냅니다.
- 0 ≤ deliveries의 원소 ≤ 50
- 0 ≤ pickups의 원소 ≤ 50
- 트럭의 초기 위치는 물류창고입니다.
입출력 예 cap n deliveries pickups result
| 4 | 5 | [1, 0, 3, 1, 2] | [0, 3, 0, 4, 0] | 16 |
| 2 | 7 | [1, 0, 2, 0, 1, 0, 2] | [0, 2, 0, 1, 0, 2, 0] | 30 |
입출력 예 설명
입출력 예 #1
- 문제 예시와 동일합니다.
입출력 예 #2
배달 및 수거할 재활용 택배 상자 개수
집 #1집 #2집 #3집 #4집 #5집 #6집 #7| 배달 | 1개 | 0개 | 2개 | 0개 | 1개 | 0개 | 2개 |
| 수거 | 0개 | 2개 | 0개 | 1개 | 0개 | 2개 | 0개 |
배달 및 수거 과정
집 #1집 #2집 #3집 #4집 #5집 #6집 #7 설명| 남은 배달/수거 | 1/0 | 0/2 | 2/0 | 0/1 | 1/0 | 0/2 | 2/0 | 물류창고에서 택배 2개를 트럭에 실어 출발합니다. |
| 남은 배달/수거 | 1/0 | 0/2 | 2/0 | 0/1 | 1/0 | 0/2 | 0/0 | 물류창고에서 7번째 집까지 이동하면서(거리 7) 7번째 집에 택배 2개를 배달합니다. |
| 남은 배달/수거 | 1/0 | 0/2 | 2/0 | 0/1 | 1/0 | 0/0 | 0/0 | 7번째 집에서 물류창고까지 이동하면서(거리 7) 6번째 집에서 빈 택배 상자 2개를 수거한 후, 수거한 빈 택배 상자를 물류창고에 내리고 택배 2개를 트럭에 싣습니다. |
| 남은 배달/수거 | 1/0 | 0/2 | 1/0 | 0/1 | 0/0 | 0/0 | 0/0 | 물류창고에서 5번째 집까지 이동하면서(거리 5) 3번째 집에 택배 1개를 배달하고, 5번째 집에 택배 1개를 배달합니다. |
| 남은 배달/수거 | 1/0 | 0/1 | 1/0 | 0/0 | 0/0 | 0/0 | 0/0 | 5번째 집에서 물류창고까지 이동하면서(거리 5) 4번째 집에서 빈 택배 상자 1개를 수거하고 2번째 집에서 빈 택배 상자 1개를 수거한 후, 수거한 빈 택배 상자를 물류창고에 내리고 택배 2개를 트럭에 싣습니다. |
| 남은 배달/수거 | 0/0 | 0/1 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 물류창고에서 3번째 집까지 이동하면서(거리 3) 1번째 집에 택배 1개를 배달하고, 3번째 집에 택배 1개를 배달합니다. |
| 남은 배달/수거 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 3번째 집에서 물류창고까지 이동하면서(거리 3) 2번째 집에서 빈 택배 상자 1개를 수거한 후, 수거한 빈 택배 상자를 물류창고에 내립니다. |
30(=7+7+5+5+3+3)의 거리를 이동하면서 모든 배달 및 수거를 마쳤습니다. 같은 거리로 모든 배달 및 수거를 마치는 다른 방법이 있지만, 이보다 짧은 거리로 모든 배달 및 수거를 마치는 방법은 없습니다.
따라서, 30을 return 하면 됩니다.
내 풀이
//최대로 실어서 제일 멀리 있는데 배달 후 , 제일 멀리 있는데서 최대한 수거
//멀리있는 곳부터 포인터를 지정해서 0/0일 경우 포인터를 -1 하도록..?
public class Solution {
public long solution(int cap, int n, int[] deliveries, int[] pickups) {
long answer = 0;
int idx = n-1;
int deliverTotalBox = 0, pickupTotalBox = 0;
for (int i = 0; i < n; i++) {
if(deliveries[i] > 0) {
deliverTotalBox+= deliveries[i];
}
if(pickups[i] > 0) {
pickupTotalBox+= pickups[i];
}
}
while(idx >= 0) {
if (deliveries[idx] == 0 && pickups[idx] == 0) {
idx--;
continue;
}
int pointer = idx;
answer += (2 * (idx + 1));
int deliverBox = cap, emptyBox = 0;
while (pointer >= 0) {
if (deliverTotalBox > 0 && deliverBox != 0 && deliveries[pointer] > 0) {
if (deliveries[pointer] >= deliverBox) {
deliveries[pointer] -= deliverBox;
deliverTotalBox -= deliverBox;
deliverBox = 0;
} else {
deliverBox -= deliveries[pointer];
deliverTotalBox -= deliveries[pointer];
deliveries[pointer] = 0;
}
}
if (pickupTotalBox > 0 && emptyBox != cap && pickups[pointer] > 0) {
if (pickups[pointer] >= (cap - emptyBox)) {
pickups[pointer] -= (cap - emptyBox);
pickupTotalBox -= (cap - emptyBox);
emptyBox = cap;
} else {
emptyBox += pickups[pointer];
pickupTotalBox -= pickups[pointer];
pickups[pointer] = 0;
}
}
if(deliveries[pointer] == 0 && pickups[pointer] == 0) {
idx--;
}
if ((deliverBox == 0 && emptyBox == cap) || (deliverTotalBox == 0 && emptyBox == cap)
|| (pickupTotalBox == 0 && deliverBox == cap) || (deliverTotalBox == 0 && pickupTotalBox == 0)) {
break;
}
pointer--;
}
}
return answer;
}
}뒤에서부터 그리디방식으로 배달 및 수거를 해야한다는 최적의 방법은 생각을 했으나,
계산 방식이 시간초과를 유발한 것 같다.
뒤에서부터 배달/수거를 cap만큼 하고, 다시 반복하는 방식이었다..!
최악의 경우 O(n^2) 라서 100,000 * 100,000 = 10,000,000,000 이다..! 🥹
굳이 다시 돌아갈 것 없이 O(n)으로 해결할 수 있는 방법이 있다.
한 지점에 와야할 횟수를 한번에 계산하면서 동시에 미리 배달할/수거할 박스를 더해놓고 초과한만큼만 빼면 된다.
처음에 코드를 보고도 이해가 잘 안갔지만, 머리를 열심히 굴려보다 깨달았다.
다른 사람 풀이를 참고한 풀이
public class Solution {
public long solution(int cap, int n, int[] deliveries, int[] pickups) {
int deliver = 0, pickup = 0;
long answer = 0;
for (int i = n-1; i >= 0; i--) {
if(deliveries[i] != 0 || pickups[i] != 0) {
int cnt = 0;
while(deliver < deliveries[i] || pickup < pickups[i]) {
cnt++;
deliver += cap;
pickup += cap;
}
deliver -= deliveries[i];
pickup -= pickups[i];
answer += (i+1) * cnt * 2;
}
}
return answer;
}
}이렇게하면 n 한번에 답을 구할 수 있다.
어쩜 이런 풀이가 ...! 머리에서 나올 수 있나..
난 아직 멀었다...ㅠㅠ
'CS > Algorithm' 카테고리의 다른 글
| [HackerRank] Lily's Homework (Java) (0) | 2023.05.18 |
|---|---|
| [백준] 3197번 - 백조의 호수 (Java) (0) | 2023.01.27 |
| [프로그래머스] 등산코스 정하기 - 22 카카오 인턴 채용 (Java) (11) | 2022.12.16 |
| [백준] 1939번 - 중량제한 (Java) (4) | 2022.07.07 |
| [백준] 1655번 - 가운데를 말해요 (c++) (0) | 2021.10.25 |
